Excelは、データの分析や計算に広く使われている表計算ソフトウェアですが、その機能は単なるデータの整理や計算にとどまりません。実は、Excelには微分を計算する方法も存在します。この記事では、Excelを使って微分を計算する方法を詳しく解説します。微分は数学において非常に重要な概念であり、変化の割合を測定するのに役立ちます。Excelの強力な機能を活用して、複雑な微分計算を効率的に行うことができます。この記事を通じて、Excelでの微分計算の方法をマスターし、あなたのデータ分析のスキルを更に磨いてください。
Excelで微分を計算する方法
Excelでは、数式を使用して微分を計算することができます。微分は、関数の変化率を測定するために使用される数学的概念であり、経済、工学、科学など、さまざまな分野で応用されます。Excelでは、数値微分を使用して、関数の微分係数を近似することができます。
数値微分の基本
数値微分は、関数の微分係数を近似するための方法です。関数f(x)の点xでの微分係数は、xの小さい変化に対するf(x)の変化の比率として定義されます。Excelでは、数値微分を実行するために、次の数式を使用できます。 =(f(x + h) – f(x)) / h ここで、hは非常に小さい数値です。一般的には、h = 0.0001などの小さい値を使用します。
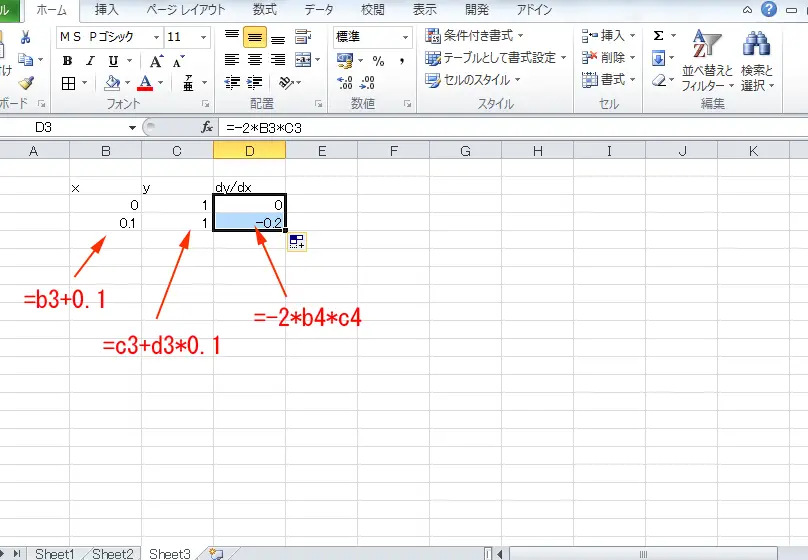
Excelで数値微分を計算する手順
1. セルA1に変数xの値を入力します。 2. セルB1に、関数f(x)を表す数式を入力します。例えば、f(x) = x^2の場合は、=A1^2と入力します。 3. セルC1に、数値微分を計算する数式を入力します。例えば、=(f(x + 0.0001) – f(x)) / 0.0001と入力します。 4. セルA1の値を変更すると、セルC1に微分係数の近似値が表示されます。
数値微分の応用例
数値微分は、変数の変化に対する関数の感度を分析するのに役立ちます。例えば、経済学では、生産量の変化に対する費用の変化率を計算するために、費用関数の微分係数を計算することがあります。
数値微分の限界
数値微分は、微分係数の近似値を提供するだけであり、正確な値ではないことに注意してください。また、hの値が非常に小さい場合、丸め誤差が発生する可能性があります。
高階微分の計算
高階微分は、関数の微分係数をさらに微分することで得られます。Excelでは、高階微分を計算するために、数値微分の手順を繰り返します。例えば、2階 微分を計算するためには、数値微分の数式を再度適用します。
| 項目 | 説明 |
| 数値微分の基本 | 関数の微分係数を近似するための方法 |
| Excelで数値微分を計算する手順 | Excelで数値微分を実行するためのステップバイステップの手順 |
| 数値微分の応用例 | 数値微分を使用して変数の変化に対する関数の感度を分析する例 |
| 数値微分の限界 | 数値微分の精度と丸め誤差に関する注意事項 |
| 高階微分の計算 | 高階微分を計算するために数値微分の手順を繰り返す方法 |
よくある質問
Excelで微分を計算するにはどのような方法がありますか?
Excelで微分を計算する方法は複数ありますが、最も一般的な方法は数値微分です。数値微分は、関数の値を近似的に計算するために、有限差分法を使用します。具体的には、非常に小さい数値変化(例えば0.0001)を使って、関数の値の変化量を計算し、その変化量を変化した数値で割ることで、微分係数を近似的に求めます。
Excelで数値微分を実行するには、どのような関数や式を使用しますか?
Excelでは、数値微分を実行するために特定の関数は用意されていませんが、基本的な演算子と関数を組み合わせて数値微分を計算できます。例えば、もしセルA1にxの値が入力され、B1に関数f(x)の式が入力されている場合、C1に以下のような式を入力することで、xにおけるf(x)の微分係数を近似的に計算できます:(f(x+0.0001)-f(x))/0.0001。
Excelで高次の微分を計算するには、どうすればよいですか?
高次の微分を計算するためには、数値微分の手法を繰り返し適用します。例えば、二階微分を計算する場合、一度目の微分で得られた微分係数を用いて、再度数値微分を行います。このプロセスを繰り返すことで、三階以上の高次微分も計算できます。ただし、微分の階数が上がるごとに、計算の誤差が蓄積されるため、注意が必要です。
Excelで微分を計算する際に、どのような注意点がありますか?
Excelで微分を計算する際の主な注意点は、数値の精度と計算の効率性です。数値微分では、非常に小さい数値変化を用いるため、丸め誤差が発生しやすくなります。この誤差を最小限に抑えるためには、適切なステップサイズ(変化量)を選択することが重要です。また、計算の効率性を高めるために、高次の微分を計算する場合には、繰り返し数値微分を行うのではなく、一度に高次の微分係数を求める方法を検討することも効果的です。

私は、生産性向上に情熱を持つデータ分析とオフィスツール教育の専門家です。20年以上にわたり、データ分析者としてテクノロジー企業で働き、企業や個人向けのExcel講師としても活動してきました。
2024年、これまでの知識と経験を共有するために、日本語でExcelガイドを提供するウェブサイト**「dataka.one」**を立ち上げました。複雑な概念を分かりやすく解説し、プロフェッショナルや学生が効率的にExcelスキルを習得できるようサポートすることが私の使命です。