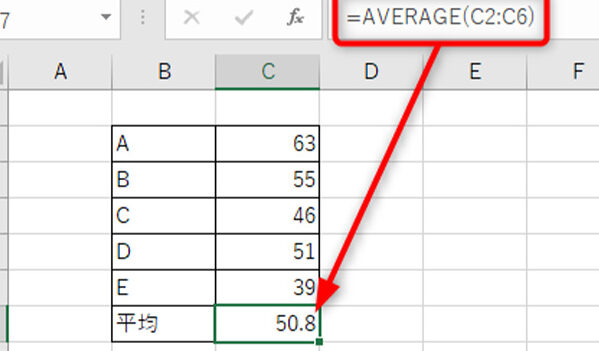
標準誤差は、データのばらつきや変動を表す重要な指標です。Microsoft Excelでは、標準誤差を簡単に計算できる機能が提供されており、データ分析の際に広く用いられています。この記事では、Excelにおける標準誤差の計算方法や、その解釈のしかたについて詳しく解説します。また、標準誤差がどのようにしてデータのばらつきを数量化しているか、そして、それが統計分析においてどのような意味を持つかについても説明します。この知識を活用することで、データ分析の精度を向上させることができます。
Excel標準誤差:データのばらつきを表す指標
Excelでの標準誤差の計算は、データのばらつきを理解する上で重要な手法です。標準誤差は、標本の平均値が母集団の真の平均値からどれだけ離れているかを示す指標として用いられます。これにより、データの信頼性や推定の精度を評価することができます。
標準誤差の計算方法
Excelでは、標準誤差を計算するために、まずデータの平均値と分散を求めます。その後、分散の平方根をとり、標本数の平方根で割ることで標準誤差を得られます。具体的な数式は以下の通りです。 標準誤差 = √(分散 ÷ 標本数)
標準誤差の解釈
標準誤差が小さい場合は、標本の平均値が母集団の平均値に近いと考えられます。これは、データの信頼性が高いことを示します。一方、標準誤差が大きい場合は、標本の平均値が母集団の平均値から離れており、データの信頼性が低い可能性があります。
標準誤差と標準偏差の違い
標準誤差と標準偏差はともにデータのばらつきを表す指標ですが、用途が異なります。標準偏差は、データが平均値からどれだけ散らばっているかを示します。一方、標準誤差は、標本の平均値が母集団の平均値からどれだけ離れているかを示します。
Excelで標準誤差を計算する関数
Excelには、標準誤差を計算するための関数が用意されています。STDEV.S関数を使用することで、データの標準偏差を計算し、それを標本数の平方根で割ることで標準誤差を得られます。また、STDEV.P関数を使用すると、母集団の標準偏差を計算できます。
標準誤差を用いた信頼区間の計算
標準誤差を用いることで、信頼区間を計算することができます。信頼区間は、母集団の真の平均値がどの範囲に存在するかを示す指標です。一般的には、平均値 ± (標準誤差 × 1.96)の範囲が95%の信頼区間として用いられます。
| 用語 | 説明 |
|---|---|
| 標準誤差 | 標本の平均値が母集団の平均値からどれだけ離れているかを示す指標 |
| 標準偏差 | データが平均値からどれだけ散らばっているかを示す指標 |
| 信頼区間 | 母集団の真の平均値がどの範囲に存在するかを示す指標 |
標準誤差とはどのようなばらつきを指しますか?
標準誤差とは、母集団の標準偏差を推定するための標本のばらつきを示す指標です。それは、標本統計量の分布の分散の平方根であり、標本の代表性を評価するために使用されます。
標準誤差の定義と計算方法
標準誤差は、標本統計量の標準偏差であり、母集団パラメーターの推定の精度を示す指標です。標準誤差は、次の式で計算されます。
- 標本標準偏差を計算する。
- 標本標準偏差を標本サイズの平方根で割る。
- その結果が標準誤差である。
標準誤差が小さいほど、標本の代表性が高いとされます。
標準誤差の重要性
標準誤差は、統計解析における推定の精度を評価するために不可欠な指標です。標準誤差を用いることで、次のような利点があります。
- 母集団の真のパラメーターからの標本統計量のばらつきを把握できる。
- 異なる標本間の比較が可能になる。
- 標本サイズが大きくなるほど、標準誤差は小さくなるため、母集団の推定精度が向上することがわかる。
標準誤差は、標本の信頼性を評価するうえで重要な役割を果たします。
標準誤差と信頼区間
標準誤差は、信頼区間の計算にも使用されます。信頼区間は、母集団パラメーターが一定の確率で含まれる範囲を示します。信頼区間は、次のように計算されます。
- 標本統計量から標準誤差の定数倍を加え、減じる。
- その結果として得られる範囲が信頼区間である。
- 一般的に、95%の信頼区間は、標本統計量±1.96 × 標準誤差で計算される。
信頼区間を用いることで、母集団パラメーターの不確実性を定量化できます。
データのばらつき具合を測るための指標は?
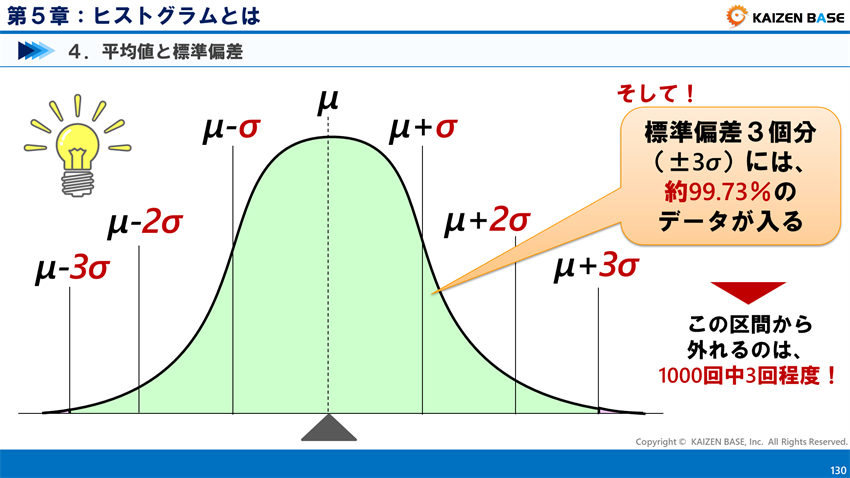
データのばらつき具合を測るための指標は、主に分散と標準偏差があります。分散はデータの各値が平均値からどれだけ離れているかを示す指標で、標準偏差は分散の平方根を取った値です。標準偏差はデータのばらつきの度合いを平均値と同じ単位で表すことができます。
分散
分散は、データの各値と平均値の差の二乗の平均です。数学的には次式で定義されます。
- データの各値と平均値の差を計算する。
- その差の二乗を取る。
- それらの二乗の平均を計算する。
このようにして計算された分散は、データが平均値からどれだけ散らばっているかを数値で表します。
標準偏差
標準偏差は、分散の平方根を取ったものです。これにより、データのばらつきの度合いを平均値と同じ単位で表すことができます。
- 分散を計算する。
- 分散の平方根を取る。
標準偏差は、データの分布が平均値からどれだけ離れているかを示し、データ解析において非常に重要な役割を果たします。
分散と標準偏差の違い
分散と標準偏差はどちらもデータのばらつき具合を測る指標ですが、次のような違いがあります。
- 分散はデータの各値と平均値の差の二乗の平均であり、単位が違う場合があります。
- 標準偏差は分散の平方根を取った値であり、データのばらつきの度合いを平均値と同じ単位で表すことができます。
- 標準偏差は分散と比較して、データのばらつき具合をより直感的に理解しやすい指標です。
これらの指標を用いることで、データの分布やばらつき具合を定量的に評価することが可能となります。
データのばらつきを表す値は何ですか?
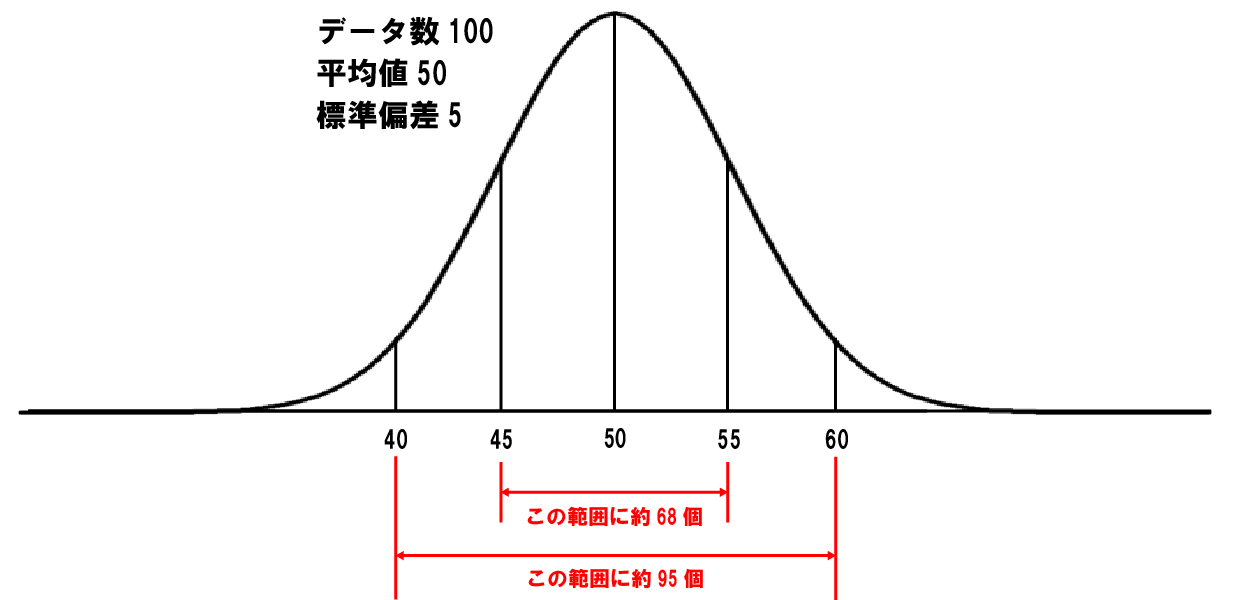
データのばらつきを表す値は、分散や標準偏差などがあります。これらの数値は、データがどれくらい広がっているかを示し、データの分布を理解するのに役立ちます。
分散
分散は、データの各値が平均からどれだけ離れているかを示す指標です。分散が大きいほど、データが平均から離れていることが多く、ばらつきが大きいことを示します。分散は次の式で計算できます。
- データの平均を計算する。
- 各データ値と平均の差を計算し、二乗する。
- これらの二乗した値の平均を求める。
標準偏差
標準偏差は、分散の平方根です。分散と同じく、データのばらつきを示す指標ですが、分散と異なり、データの単位と同じ単位で表されます。標準偏差が大きいほど、データのばらつきが大きいことを示します。標準偏差は次の式で計算できます。
- 分散を計算する。
- 分散の平方根を求める。
範囲
範囲は、データの最大値と最小値の差です。範囲が大きいほど、データのばらつきが大きいことを示します。しかし、範囲はデータの最大値と最小値しか考慮しないため、外れ値の影響を強く受けるという欠点があります。範囲は次の式で計算できます。
- データの最大値を求める。
- データの最小値を求める。
- 最大値と最小値の差を計算する。
データのばらつきを示すグラフは?
データのばらつきを示すグラフは、箱ひげ図(ボックスプロット)です。箱ひげ図は、データの平均値、中央値、四分位数、最大値、最小値などの要素を示すことができます。また、データの分布の形状や外れ値の有無も把握できます。
箱ひげ図の読み方
箱ひげ図は、データの分布を視覚化するグラフです。以下の要素を含んでいます。
- 箱(ボックス):データの第1四分位数(25パーセント点)から第3四分位数(75パーセント点)までの範囲を示します。
- 中央値:データの真ん中の値を表し、箱の中央に線で表示されます。
- ひげ:箱から伸びる線で、データの最大値と最小値までを示します。ただし、外れ値は除外されます。
箱ひげ図の利点
箱ひげ図は、データのばらつきを把握するのに非常に役立ちます。以下のような利点があります。
- データの分布が一目でわかる:箱ひげ図は、データの分布の形状を視覚的に表現するため、データの特徴を把握しやすいです。
- 外れ値の検出が容易:箱ひげ図では、外れ値が点で表示されるため、データに異常値が含まれているかどうかをすぐに確認できます。
- グループ間の比較ができる:複数のデータセットを同時に表示することで、データ間の違いを簡単に比較できます。
箱ひげ図の作成方法
箱ひげ図を作成するには、以下の手順を踏みます。
- データを整理する:まず、データを昇順または降順に並べ替えます。
- 四分位数を求める:第1四分位数(25パーセント点)、第2四分位数(中央値)、第3四分位数(75パーセント点)を求めます。
- 箱を描く:第1四分位数から第3四分位数までの範囲を箱で表します。中央値は箱の中央に線で示します。
- ひげを描く:箱から最大値と最小値まで線を引きます。外れ値は点で表示します。
よくある質問
標準誤差とは何ですか?
標準誤差は、データのばらつきを表す指標の一つで、標本の平均値が母集団の平均値からどれだけ離れているかを示すものです。言い換えれば、標本の平均値を用いて母集団の平均値を推定するときの不確実性の度合いを表します。統計解析では、標準誤差は母集団のパラメータを推定する際の信頼性を評価するために用いられます。
Excelで標準誤差を計算する方法を教えてください。
Excelで標準誤差を計算するには、STDEV.S関数またはSTDEV.P関数を使用します。STDEV.S関数は、標本標準偏差を計算します。一方、STDEV.P関数は、母集団標準偏差を計算します。標準誤差を求めるには、標本標準偏差を標本数の平方根で割ります。例えば、標本標準偏差が10、標本数が100の場合、標準誤差は10÷√100 = 1となります。
標準誤差と標準偏差の違いは何ですか?
標準誤差と標準偏差はどちらもデータのばらつきを表す指標ですが、その目的が異なります。標準偏差は、データそのもののばらつきを測るために使用されます。一方、標準誤差は、標本平均値が母集団平均値からどれだけ離れているかを示すもので、標本による推定の不確実性を表します。標準偏差は母集団や標本のデータのばらつきを評価するのに対し、標準誤差は標本平均値の推定精度を評価するために用いられます。
標準誤差が大きい場合はどう解釈すべきなですか?
標準誤差が大きい場合は、標本平均値の推定精度が低いと解釈されます。これは、標本が母集団を代表していない可能性が高いことを意味します。そのため、標準誤差が大きい場合には、データの信頼性や解析結果の解釈に注意を要し、より多くのデータを収集するか、標本抽出方法を見直すことが求められます。

私は、生産性向上に情熱を持つデータ分析とオフィスツール教育の専門家です。20年以上にわたり、データ分析者としてテクノロジー企業で働き、企業や個人向けのExcel講師としても活動してきました。
2024年、これまでの知識と経験を共有するために、日本語でExcelガイドを提供するウェブサイト**「dataka.one」**を立ち上げました。複雑な概念を分かりやすく解説し、プロフェッショナルや学生が効率的にExcelスキルを習得できるようサポートすることが私の使命です。