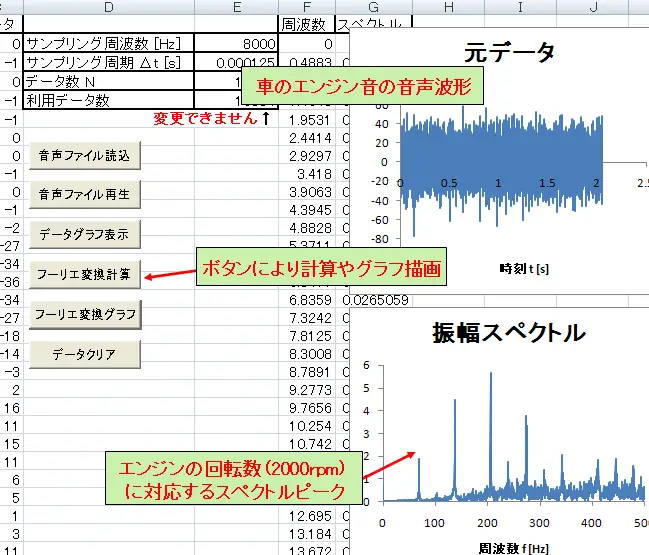
「」は、データ解析において重要な手法であるフーリエ変換を、手軽にExcelで行う方法を解説する記事です。フーリエ変換は、信号を周波数成分に分解することで、データの特徴を捉えることができるため、音声や画像の処理、時系列データの解析など、多くの分野で活用されています。本記事では、Excelの分析ツールを使って、フーリエ変換の手順をわかりやすく説明します。また、具体的な例を用いて、フーリエ変換の結果を解釈する方法も紹介します。この記事を通じて、Excelでフーリエ変換を効率的に行う方法を学び、データ解析の力を向上させることを目的としています。
Excelでフーリエ変換を使ってデータを分析する
Excelでは、フーリエ変換を利用してデータ解析を行うことができます。この機能を使うことで、時系列データなどの周期性を分析し、データの特徴を捉えることが可能です。
フーリエ変換とは
フーリエ変換は、時系列データや空間データを周波数領域に変換する手法です。これにより、データの周期的な構造を把握することができます。Excelでは、フーリエ変換を用いてデータの周波数分析を行うことができます。
| 項目 | 説明 |
| フーリエ変換の目的 | 時系列データの周期性を分析する |
| 適用分野 | 音声、画像、経済指標などの解析 |
Excelでのフーリエ変換の手順
Excelでは、データ解析のためのアドイン「分析ツール」を使用してフーリエ変換を行います。以下の手順で操作を行ってください。
- 「データ」タブから「分析ツール」を開く
- 「フーリエ解析」を選択し、入力データ範囲を指定する
- 出力先を指定し、「OK」をクリックする
フーリエ変換の結果の解釈
フーリエ変換の結果は、複素数の形で表示されます。実数部と虚数部からなる周波数成分を解析することで、データの周期的な特徴を把握できます。
| 項目 | 説明 |
| 実数部 | 周波数成分の強度 |
| 虚数部 | 周波数成分の位相情報 |
Excelのフーリエ変換の活用例
Excelのフーリエ変換を用いることで、様々なデータの周期性を分析することができます。例えば、経済指標の分析や、音声データの特徴抽出などに活用できます。
- 株価の時系列データ分析
- 音声データの周波数解析
- 気象データの周期性の解析
フーリエ変換の注意点
フーリエ変換を行う際には、データの長さやサンプリング間隔に注意が必要です。また、データに含まれるノイズや外れ値にも配慮し、適切な前処理を行ってください。
| 項目 | 注意点 |
| データの長さ | 2のべき乗にすることが望ましい |
| サンプリング間隔 | 一定である必要がある |
| ノイズや外れ値 | 適切な前処理を行う |
ExcelでFFTできる上限は?

ExcelでFFTできる上限は、デフォルトで設定されている最大データポイント数によって異なります。Excel 2016以降のバージョンでは、1,048,576行のデータを処理できるため、最大でこの数のデータポイントまでFFTを実行できます。しかし、実際には、コンピュータの性能や利用可能なメモリ量によって、処理できる最大データポイント数は異なる場合があります。
ExcelでFFTを実行するためのデータ準備
ExcelでFFTを実行する前に、データを適切に準備することが重要です。おおまかに言うと、以下の手順を実行します。
- データを時系列データとして整理します。
- データに隙間や抜けがないことを確認します。FFTは等間隔のデータを前提としているため、データに抜けがあると結果が正確でなくなることがあります。
- データがリアル数であることを確認します。ExcelのFFTツールは、複素数データは処理できません。
ExcelでFFTを実行する方法
ExcelでFFTを実行するためには、データ分析ツールを使います。このツールは、Excelのアドインとして提供されています。以下の手順でFFTを実行できます。
- データ分析ツールをインストールし、有効にします。
- 「データ」タブから「データ分析」を選択し、「フーリエ解析」を選択します。
- 解析対象のデータ範囲を選択し、出力先を指定して「OK」をクリックします。
ExcelでFFTの結果を解釈する方法
FFTの結果は、複素数の形で出力されます。実数部と虚数部、それぞれの値が表で示されます。結果を解釈するためには、以下の点に注意してください。
- 実数部と虚数部の値から、振幅と位相を計算できます。
- 複素数の絶対値(振幅)は、実数部と虚数部の二乗和の平方根です。
- 位相は、実数部と虚数部から算出される、偏角です。
周波数解析とフーリエ変換の違いは何ですか?
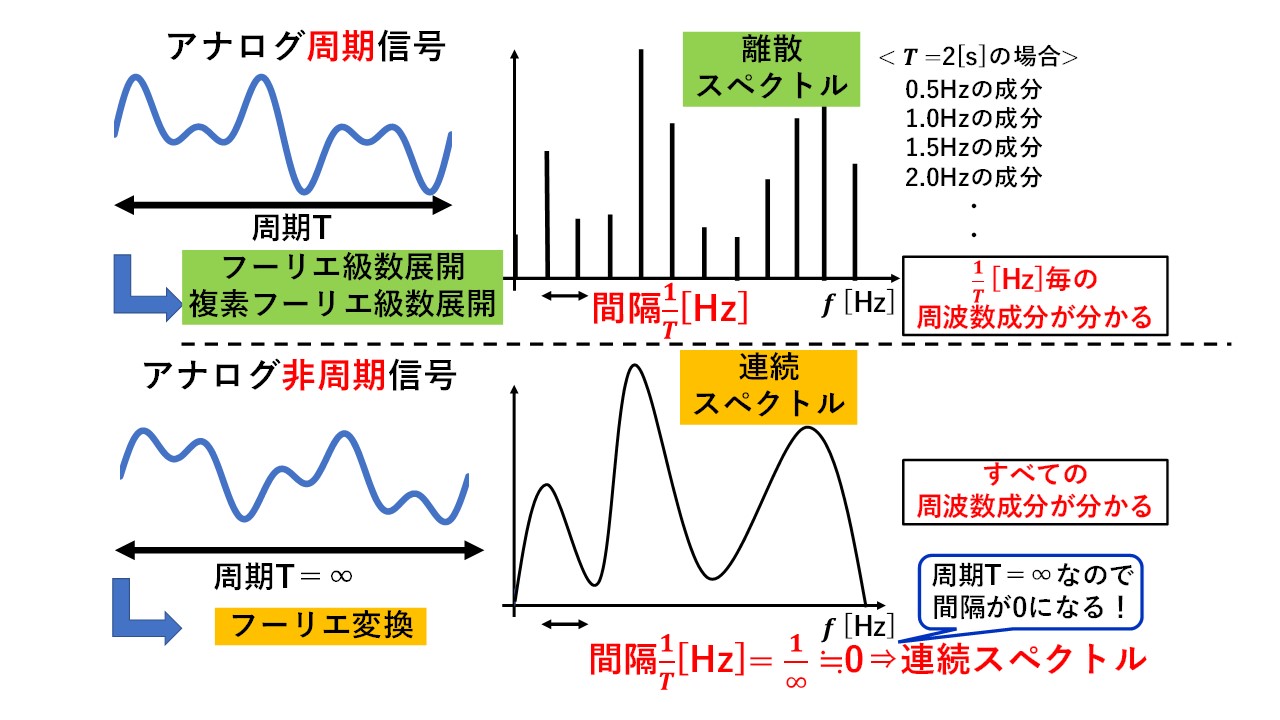
周波数解析とフーリエ変換の違いは、周波数解析は信号を周波数領域で解析する一般的な手法であり、フーリエ変換は周波数解析を行うための特定の数学的ツールです。フーリエ変換は、時間領域の信号を周波数領域の信号に変換することができます。これにより、信号の周波数成分を明らかにし、解析を容易にします。
周波数解析とは何か
周波数解析は、時間領域の信号を周波数領域で解析する手法です。これにより、信号の周波数特性を明らかにし、信号の理解や処理を容易にします。
- 周波数解析は、信号の周波数成分を特定することができます。
- 信号のノイズ除去やフィルタリングに役立ちます。
- 音声や画像などの信号処理分野で広く使われています。
フーリエ変換の役割
フーリエ変換は、周波数解析を行うための基本的な数学的ツールです。時間領域の信号を周波数領域の信号に変換することができます。
- フーリエ変換は、信号を正弦波と余弦波の和として表現します。
- 離散フーリエ変換(DFT)や高速フーリエ変換(FFT)は、デジタル信号処理で広く使用されています。
- フーリエ変換を用いることで、信号の周波数スペクトルを得ることができます。
周波数解析とフーリエ変換の関連性
周波数解析は、信号を周波数領域で解析する一般的な手法であり、フーリエ変換はそのための数学的ツールの一つです。
- フーリエ変換は、周波数解析を行うための基本的な手法です。
- 周波数解析では、フーリエ変換を用いて信号の周波数成分を特定します。
- フーリエ変換は、周波数解析の枠組みの中で広く応用されています。
FFT分析とは?
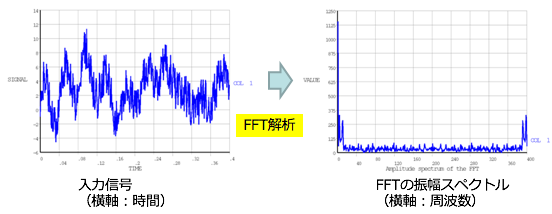
FFT分析とは、高速フューリエ変換(Fast Fourier Transform)を用いた信号解析の手法です。FFTは、デジタル信号処理において、時間領域の信号を周波数領域に変換する際に用いられるアルゴリズムであり、ディジタル信号を周波数成分に分解することができます。これにより、信号の周波数特性やスペクトルを解析することが可能となります。
FFT分析の原理と特徴
FFT分析は、フューリエ変換を高速化したアルゴリズムを用いて、時間領域の信号を周波数領域に変換します。この変換を通じて、信号の周波数成分を明らかにし、スペクトル解析を行うことができます。FFTの特徴は以下の通りです。
- 高速性: FFTは、フューリエ変換を効率的に計算することができるため、高速な信号解析が可能です。
- 周波数解像度: FFT分析では、サンプリング周波数とデータ長に応じて、周波数解像度が決定されます。
- 応用範囲の広さ: 音声、画像、振動などのさまざまな信号に対して適用可能であり、多くの分野で利用されています。
FFT分析の適用分野
FFT分析は、様々な分野での信号解析に適用されています。以下に代表的な適用分野を挙げます。
- 音声信号処理: 音声の周波数特性を解析し、音声の识别や変換、ノイズ除去などに利用されます。
- 画像処理: 画像の周波数特性を解析し、画像フィルタリング、圧縮、解析などに適用されます。
- 振動解析: 機械や構造物の振動データを解析し、故障診断や振動特性の評価に役立ちます。
FFT分析の注意点
FFT分析を行う際には、以下の点に注意する必要があります。
- サンプリング周波数: 信号を適切にサンプリングするために、サンプリング周波数は信号の最高周波数の2倍以上である必要があります(ナイキストの定理)。
- 窓関数: 有限長の信号を解析する際には、窓関数を適用して周波数漏れを低減することが重要です。
- ゼロパディング: データ長を増やすことで周波数解像度を向上させる手法ですが、過度なゼロパディングは計算量の増加を引き起こすため、適切な長さを選択することが重要です。
フーリエ変換で画像処理をすると何がわかる?

フーリエ変換を用いた画像処理では、画像の周波数領域での特徴を明らかにすることができます。具体的には、画像のエッジ、テクスチャ、ノイズなどの情報を周波数領域で捉えることができます。これにより、画像の特徴を抽出したり、ノイズ除去や画像補正を行ったりすることが可能になります。
周波数領域での画像の特徴抽出
フーリエ変換により、画像の空間領域から周波数領域への変換が行われます。これにより、画像のエッジやテクスチャなどの情報が周波数成分として表現されます。例えば、低周波数成分は画像の全体的な明るさや色調を表し、高周波数成分は細かなテクスチャやエッジの情報を含んでいます。
- 低周波数成分:画像の全体的な明るさや色調
- 中周波数成分:画像のテクスチャや模様
- 高周波数成分:画像のエッジや細かな詳細
ノイズ除去
フーリエ変換を用いて、画像のノイズ成分を周波数領域で特定し、除去することができます。ノイズは一般的に高周波数成分として現れるため、適切なフィルタリングを行うことでノイズを抑制することが可能です。
- ノイズの周波数成分を特定
- 適切なフィルタ(ローパスフィルタなど)を適用
- ノイズ除去された画像をフーリエ逆変換で復元
画像補正
フーリエ変換を用いることで、画像のぼけや歪みを補正することができます。例えば、モーションブラーやアウトオブフォーカスなどによるぼけは、周波数領域での特定の成分を調整することで補正が可能です。
- ぼけや歪みの原因となる周波数成分を特定
- 適切なフィルタ(ハイパスフィルタなど)を適用
- 補正された画像をフーリエ逆変換で復元
フーリエ変換は、画像処理における強力な手法の一つであり、周波数領域での画像の特徴を理解することで、さまざまな画像処理タスクに応用することができます。
よくある質問
Excelでフーリエ変換はどのように行いますか?
Excelでフーリエ変換を行うには、まずデータを入力し、次に「データ」タブの「分析」グループで「データ分析」をクリックします。そして、「フーリエ解析」を選び、変換したいデータの範囲を選択します。これにより、時間領域のデータが周波数領域のデータに変換されます。
Excelのフーリエ変換を使うには、どのような準備が必要ですか?
Excelのフーリエ変換を使うためには、まず分析ツールアドインをインストールする必要があります。これは、Excelの「ファイル」タブから「オプション」を選択し、「アドイン」で「Excel アドイン」を選び、そして「分析ツール」をチェックして「OK」をクリックすることで行えます。
フーリエ変換後のデータはどのように解釈しますか?
フーリエ変換後のデータは、元の時間領域のデータから周波数領域に変換されたものです。変換後のデータは、異なる周波数成分の強さを示しており、これを使って周期的なパターンやノイズを分析することができます。
Excelのフーリエ変換にどのような制限がありますか?
Excelのフーリエ変換にはいくつかの制限があります。まず、データポイントの数は2のべき乗でなければなりません(例:256、512、1024)。また、フーリエ変換は複素数を扱うことができないため、実数データのみに適用できます。これらの制限を考慮して、データの前処理や解析方法を適切に選択する必要があります。

私は、生産性向上に情熱を持つデータ分析とオフィスツール教育の専門家です。20年以上にわたり、データ分析者としてテクノロジー企業で働き、企業や個人向けのExcel講師としても活動してきました。
2024年、これまでの知識と経験を共有するために、日本語でExcelガイドを提供するウェブサイト**「dataka.one」**を立ち上げました。複雑な概念を分かりやすく解説し、プロフェッショナルや学生が効率的にExcelスキルを習得できるようサポートすることが私の使命です。