カイ二乗検定は、統計解析において頻繁に使用される手法の一つです。この検定は、観察されたデータが理論上の分布に適合しているかどうか、あるいは二つの変数間に関連性があるかどうかを評価するために用いられます。特に、Excelを使用することで、複雑な計算を簡単に行うことができ、手間と時間を大幅に削減できます。この記事では、Excelを使用してカイ二乗検定を行う方法を詳しく説明し、手順を追って理解を深めます。また、実際のデータを用いた例も取り上げ、検定の適用方法を具体的に見ていきます。
Excel カイ二乗検定:カイ二乗検定を行う方法
Excelでカイ二乗検定を実行する方法について詳しく説明します。カイ二乗検定は、観察されたデータが理論的に期待される分布と目に見えて異なるかどうかを判断するための統計的手法です。この検定は、カテゴリカルデータの分析に広く使用されています。
カイ二乗検定の基本
カイ二乗検定は、観察された頻度と期待される頻度との間の差を調べることで、データの分布が特定の仮説と一致しているかどうかを判断します。この検定では、次の仮説を検定します。 – 帰無仮説(H0) : 観察されたデータは期待される分布に一致する。 – 対立仮説(H1) : 観察されたデータは期待される分布と一致しない。
Excelでのカイ二乗検定の設定
Excelでは、CHISQ.TEST関数を使用してカイ二乗検定を実行できます。この関数では、観察された頻度と期待される頻度の2つの範囲を指定します。 excel =CHISQ.TEST(観察された頻度の範囲, 期待される頻度の範囲) この関数は、観察されたデータと期待されるデータとの間のカイ二乗統計量と、それに対応するP値を返します。
データの準備
カイ二乗検定を行う前に、データを適切な形式に整理する必要があります。一般的には、次のようにデータを表形式で整理します。
| カテゴリ | 観察された頻度 | 期待される頻度 |
|---|---|---|
| カテゴリ1 | 10 | 12 |
| カテゴリ2 | 20 | 18 |
| カテゴリ3 | 15 | 15 |
この表では、カテゴリごとに観察された頻度と期待される頻度が示されています。
P値の解釈
カイ二乗検定の結果として得られるP値は、帰無仮説が正しい場合に、観察されたデータと期待されるデータとの間の差が偶然に発生する確率を示します。一般的には、P値が0.05以下の場合、帰無仮説を棄却し、観察されたデータが期待される分布と目に見えて異なるとして判断します。
Excelでのカイ二乗検定の実行例
Excelでカイ二乗検定を実行する手順を例で示します。 1. 観察された頻度と期待される頻度のデータを表に整理します。 2. CHISQ.TEST関数を使用して、カイ二乗統計量とP値を計算します。 excel =CHISQ.TEST(A2:A4, B2:B4) 3. P値を解釈し、帰無仮説を棄却するかどうかを判断します。 このように、Excelを使用すると、簡単にカイ二乗検定を行うことができます。
カイ二乗検定をExcelでするにはどうすればいいですか?

カイ二乗検定をExcelでするには、以下の手順を実行します。
カイ二乗検定の基本
カイ二乗検定は、観察されたデータと期待されるデータとの違いを調べるための統計的方法です。この検定は、確率変数が特定の分布に従っているかどうかを判断するのに役立ちます。Excelでは、CHISQ.TEST関数を使用してカイ二乗検定を実行できます。
CHISQ.TEST関数の使い方
Excelでのカイ二乗検定には、CHISQ.TEST関数を使用します。以下のリストは、この関数を使用するための手順です。
- データを入力し、観察値と期待値の2つのテーブルを作成します。
- CHISQ.TEST関数を入力します。関数の形式はCHISQ.TEST(実際の範囲, 期待の範囲)です。
- 実際の範囲に観察値のデータ範囲を指定し、期待の範囲に期待値のデータ範囲を指定します。
カイ二乗検定の結果の解釈
CHISQ.TEST関数は、P値を返します。このP値を用いて、観察値と期待値がどの程度異なるかを判断します。以下のリストは、P値の解釈方法です。
- P値が小さいほど、観察値と期待値の違いが大きいことを示します。
- 一般に、P値が0.05以下の場合、観察値と期待値の違いが統計的に有意であると判断されます。
- P値が0.05以上の場合、観察値と期待値の違いは偶然の産物と見なされます。
検定のχ2検定の方法は?
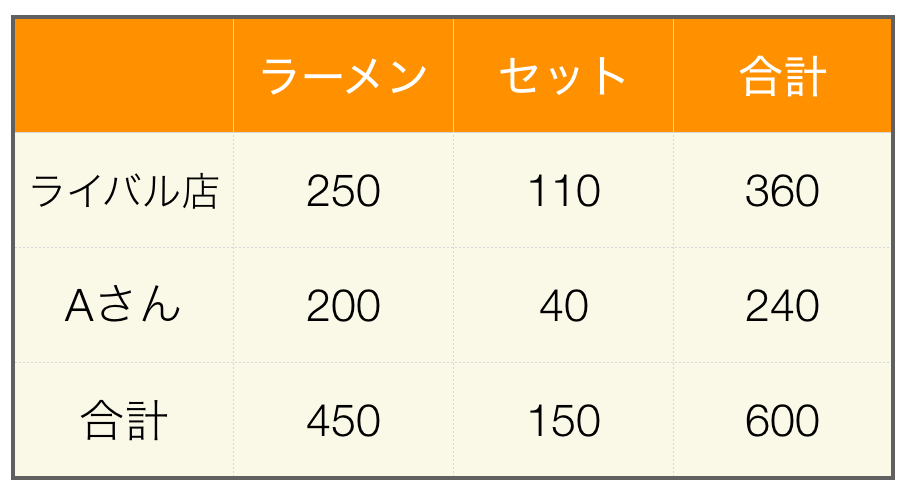
カイ二乗検定(χ2検定)は、観察されたデータが一定の仮説に従って分布しているかどうかを検定するための統計的手法です。主に、カテゴリ変数の独立性や適合度を検定するために使用されます。
カイ二乗検定の手順
カイ二乗検定を行うには、以下の手順を踏みます。
- 仮説を設定します。帰無仮説(H0)と対立仮説(H1)を定めます。
- データを集め、観察値と期待値を計算します。期待値は、帰無仮説が正しいと仮定した場合に期待される値です。
- カイ二乗統計量(χ2値)を計算します。χ2値は、観察値と期待値の差の二乗を期待値で割ったものの合計です。
- χ2値と自由度に基づいて、p値を求めます。p値は、帰無仮説が正しいと仮定した場合に、χ2値が観察された値以上になる確率です。
- p値を基に、帰無仮説を棄却するか否かを決定します。一般に、p値が有意水準(例:0.05)より小さい場合、帰無仮説を棄却します。
カイ二乗検定の適用範囲
カイ二乗検定は、以下のような状況で適用されます。
- カテゴリ変数の独立性の検定:2つのカテゴリ変数が独立であるかどうかを検定します。例えば、性別と好きなスポーツの関係など。
- 適合度の検定:観察されたデータが特定の分布(例:正規分布)に適合しているかどうかを検定します。
- 母比率の検定:母集団の比率が特定の値に等しいかどうかを検定します。
カイ二乗検定の注意点
カイ二乗検定を実施する際には、以下の注意点に留意してください。
- 標本の大きさ:標本が小さい場合、カイ二乗検定の結果は信頼性が低くなります。一般に、 EXPECTが5以上になるように標本を確保することが望ましいです。
- 標本の独立性:カイ二乗検定では、標本が互いに独立であることが前提となります。標本間に相関がある場合、検定の結果は信頼性が低くなります。
- カテゴリーの数:カテゴリーの数が多い場合、カイ二乗検定の検出力が低くなることがあります。その場合は、カテゴリーを統合するなどして検定を実施することが望ましいです。
カイ二乗検定を行う際に使用する関数はどれですか?
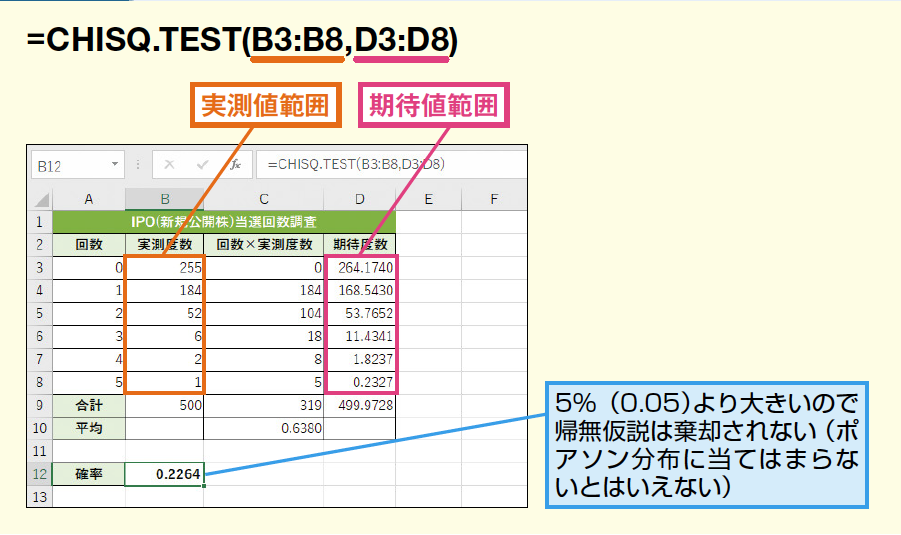
カイ二乗検定を行う際に使用する関数は、一般的にカイ二乗分布に関連するものです。特に、チスクエア関数やカイ二乗統計量を計算する関数が用いられます。
カイ二乗分布の性質
カイ二乗分布は、多くの統計的推論で用いられる連続確率分布です。以下のような特徴があります。
- カイ二乗分布は、自由度というパラメータで特徴付けられます。
- 非負の値のみをとり、正のスケールで偏った分布をしています。
- 自由度が大きくなるほど、正規分布に近づいていきます。
チスクエア関数の計算
チスクエア関数は、観測値と期待値の差を評価するために用いられます。以下の手順で計算されます。
- 観測値と期待値の差を計算します。
- この差を二乗します。
- 二乗した値を期待値で割ります。
- これらの値を全て足し合わせます。
カイ二乗検定の適用範囲
カイ二乗検定は、以下のような状況で広く用いられます。
- カテゴリーデータの独立性の検定。
- 確率分布の適合度の検定(例えば、正規分布にデータが適合しているかどうかを検定)。
- 二つの母集団の割合の差の検定。
カイ二乗検定のp値を求めるには?
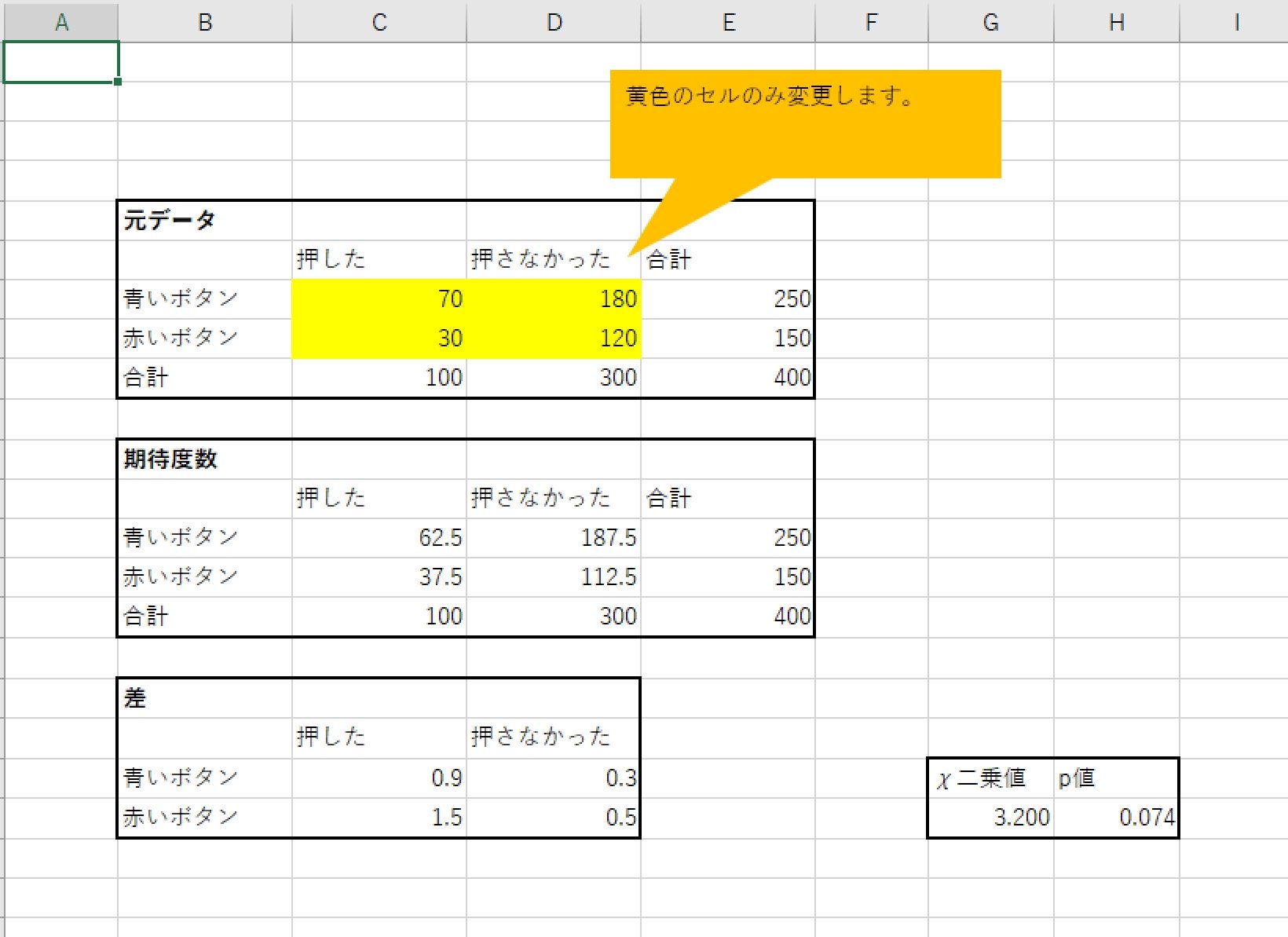
カイ二乗検定のp値を求めるには、以下の手順に従います。
カイ二乗検定の基本概念
カイ二乗検定は、観察されたデータが理論上の分布にどれくらい適合しているかを評価するための統計的手法です。この検定では、観察された度数と期待度数の差を基にして、カイ二乗統計量を計算します。その後、この統計量を用いて、p値を求めます。p値は、帰無仮説が正しいとした場合に、観察されたデータやそれより極端なデータが得られる確率を示します。
カイ二乗統計量の計算方法
カイ二乗統計量(χ²)は、以下の式で計算されます。
- 観察度数(O)と期待度数(E)を求める。
- それぞれのカテゴリについて、(O – E)² / E を計算する。
- すべてのカテゴリについて計算した値を合計する。この合計がカイ二乗統計量である。
p値の求め方
カイ二乗統計量が求まれば、p値を求めることができます。p値を求める方法は以下の通りです。
- 自由度(df)を求める。自由度は、カテゴリの数から1を引いた値である。
- カイ二乗分布表を使用して、求めたカイ二乗統計量と自由度に対応するp値を探す。
- p値が有意水準(一般的には0.05)よりも小さい場合、帰無仮説を棄却し、観察されたデータが理論上の分布と significantly difference があると結論づける。
よくある質問
カイ二乗検定とは何ですか?
カイ二乗検定は、統計学において、観察されたデータが理論的な分布に適合しているかどうかを評価するための検定です。この検定は、事象の独立性や適合度を調べるために使用されます。具体的には、観察された頻度と期待される頻度との差を基に、カイ二乗統計量を計算し、それを基に有意性を判断します。
Excelでカイ二乗検定を行うにはどうしたらいいですか?
Excelでは、CHISQ.TEST関数を使用してカイ二乗検定を行うことができます。この関数は、観察された頻度と期待される頻度の2つの範囲を引数として取り、P値を返します。P値が有意水準(通常は0.05)よりも小さい場合、観察されたデータと期待されるデータの差が偶然の範囲を超えていると判断され、帰無仮説が棄却されます。
カイ二乗検定の仮説はどのように設定しますか?
カイ二乗検定では、通常、帰無仮説として「観察されたデータと期待されるデータ之间に有意な差がない」と設定します。一方、対立仮説は「観察されたデータと期待されるデータの間に有意な差がある」とします。検定の結果、P値が有意水準よりも小さい場合、帰無仮説が棄却され、対立仮説が支持されます。
カイ二乗検定の適用条件は何ですか?
カイ二乗検定を適用するためには、いくつかの条件を満たす必要があります。まず、観察されたデータは独立であること、つまり、一つの事象の発生が別の事象の発生に影響を与えないことです。また、十分なサンプル数が必要です。一般的に、各カテゴリでの期待される頻度が5以上であることが望ましいです。これらの条件が満たされない場合、カイ二乗検定の結果は信頼性が低くなる可能性があります。

私は、生産性向上に情熱を持つデータ分析とオフィスツール教育の専門家です。20年以上にわたり、データ分析者としてテクノロジー企業で働き、企業や個人向けのExcel講師としても活動してきました。
2024年、これまでの知識と経験を共有するために、日本語でExcelガイドを提供するウェブサイト**「dataka.one」**を立ち上げました。複雑な概念を分かりやすく解説し、プロフェッショナルや学生が効率的にExcelスキルを習得できるようサポートすることが私の使命です。

