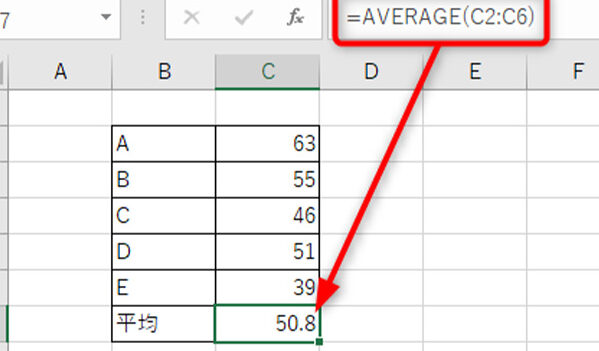
標準偏差は、データのばらつきを表す指標としてよく使われます。Excelでは、標準偏差を簡単に求めることができる機能があります。この記事では、Excelを使って標準偏差を求める方法について説明します。まず、標準偏差を求めるための関数と、その使い方を解説します。次に、計算式を使って標準偏差を求める方法も紹介します。これらの方法をマスターすることで、データの分析が効率的になります。
標準偏差を求める方法Excel:関数と計算式
Excelでは、標準偏差を求める方法として、関数と計算式の2つの方法があります。以下では、それぞれの方法について詳しく説明します。
標準偏差を求める関数:STDEV.PとSTDEV.S
Excelでは、標準偏差を求めるために、STDEV.P関数とSTDEV.S関数が用意されています。
| STDEV.P | 母集団の標準偏差を求める |
| STDEV.S | 標本の標準偏差を求める |
これらの関数を使用することで、データの標準偏差を簡単に求めることができます。
標準偏差の計算式
標準偏差を求める計算式は、以下の通りです。
| 母集団の標準偏差 | σ = √(Σ(x – μ)² / N) |
| 標本の標準偏差 | s = √(Σ(x – x̄)² / (n – 1)) |
ここで、xはデータ、μは母集団の平均、x̄は標本の平均、Nは母集団のデータ数、nは標本のデータ数を表します。
Excelで標準偏差を求めるステップ
1. データをExcelに入力する 2. 標準偏差を求める関数(STDEV.PまたはSTDEV.S)を選択する 3. 関数の引数にデータ範囲を指定する 4. Enterキーを押して結果を求める これらのステップに従って、Excelで標準偏差を簡単に求めることができます。
標準偏差を求める際の注意点
標準偏差を求める際には、以下の点に注意してください。
- 母集団と標本で使う関数が異なるので、目的によって適切な関数を選ぶ
- データに抜けや誤りがないか確認する
- 計算結果が妥当であるか検討する
標準偏差の解釈
標準偏差は、データのばらつきを表す指標です。標準偏差が大きいほどデータのばらつきが大きく、小さいほどばらつきが小さいことを示します。 標準偏差を用いることで、データの特性や分散を理解し、統計解析や予測に役立てることができます。
Excelで標準偏差を求める関数は?
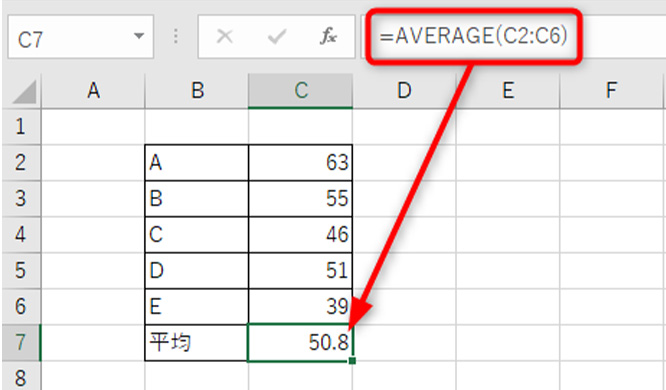
Excelで標準偏差を求める関数はSTDEV.PとSTDEV.Sです。
STDEV.P関数
STDEV.P関数は、母集団の標準偏差を求めるために使用します。この関数は、データが母集団全体であると仮定して標準偏差を計算します。
- 構文: STDEV.P(数値1, [数値2], …)
- 引数: 数値1は必須で、数値2以降は任意です。引数には、数値、配列、または数値を含む範囲を指定できます。
- 例: =STDEV.P(A1:A10) – セルA1からA10までのデータの母集団標準偏差を求めます。
STDEV.S関数
STDEV.S関数は、標本の標準偏差を求めるために使用します。この関数は、データが母集団からの標本であると仮定して標準偏差を計算します。
- 構文: STDEV.S(数値1, [数値2], …)
- 引数: 数値1は必須で、数値2以降は任意です。引数には、数値、配列、または数値を含む範囲を指定できます。
- 例: =STDEV.S(A1:A10) – セルA1からA10までのデータの標本標準偏差を求めます。
標準偏差の計算方法の違い
母集団標準偏差と標本標準偏差の計算方法には若干の違いがあります。
- 母集団標準偏差: データが母集団全体であると仮定し、分散を求める際にnで割ります。
- 標本標準偏差: データが母集団からの標本であると仮定し、分散を求める際にn-1で割ります。
- 選択性: データが母集団全体であることが明確な場合はSTDEV.Pを、データが母集団からの標本である場合はSTDEV.Sを使用します。
標準偏差の計算方法は?
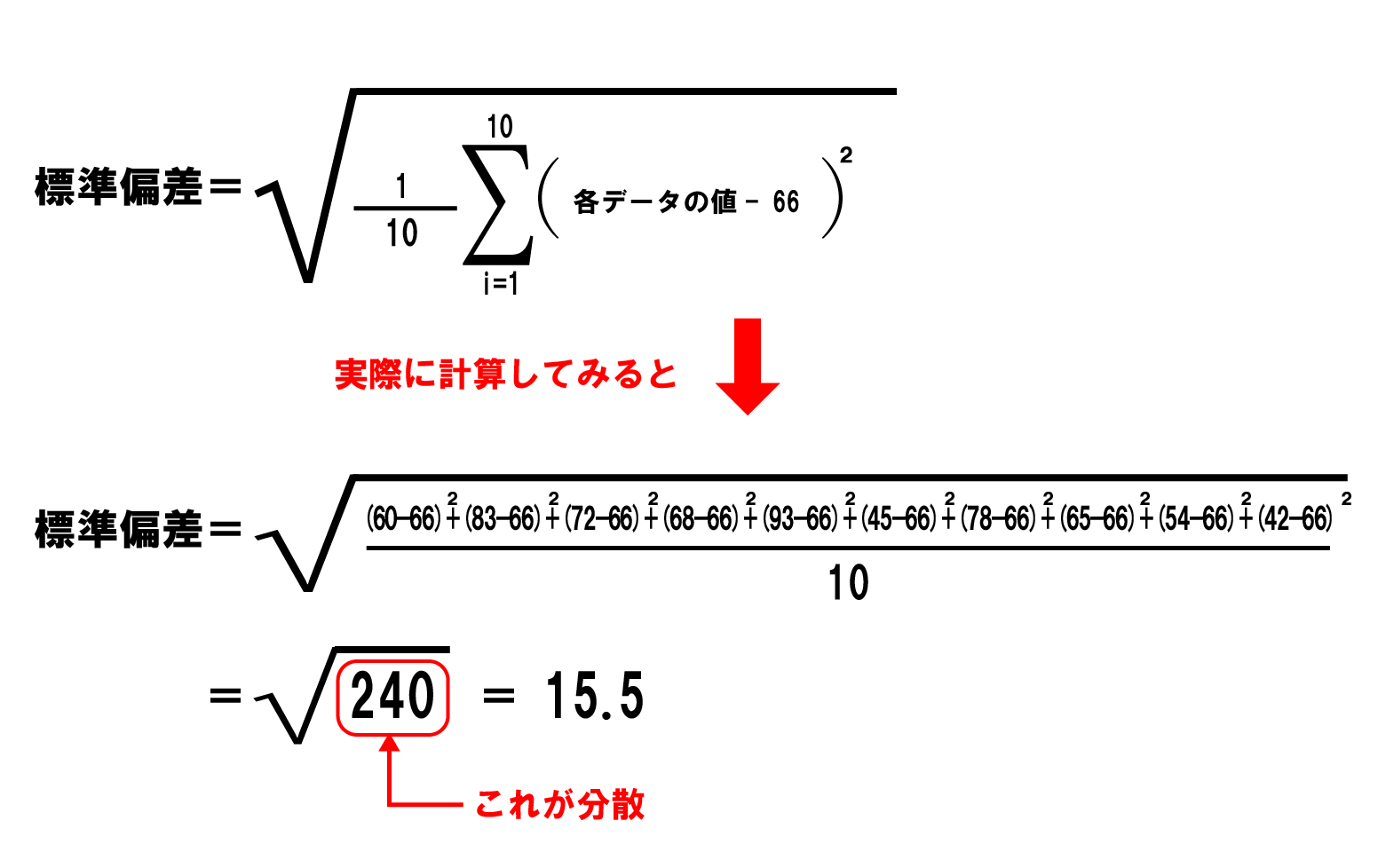
標準偏差の計算方法は、データのばらつきを測る指標であり、次の手順で計算できます。
データの平均の計算
まず、データの平均を計算します。この平均を $bar{x}$ とします。データが $x_1, x_2, ldots, x_n$ の場合、平均は次の式で計算されます。
[ bar{x} = frac{1}{n} sum_{i=1}^n x_i ]
偏差の二乗の計算
次に、各データからの偏差を計算し、それを二乗します。偏差は、データから平均を引いた値です。それぞれのデータ $x_i$ について、偏差の二乗 $(x_i – bar{x})^2$ を計算します。
- 各データから平均を引く
- その結果を二乗する
- すべてのデータに対してこの手順を繰り返す
標準偏差の計算
最後に、標準偏差を計算します。まず、偏差の二乗の平均を計算し、これを分散とします。そして、分散の平方根を取ることで標準偏差が得られます。すなわち、標準偏差 $s$ は次の式で計算されます。
[ s = sqrt{frac{1}{n} sum_{i=1}^n (x_i – bar{x})^2} ]
関数のSTDEVとは?

関数のSTDEVとは、統計学における標準偏差を計算するための関数です。標準偏差は、データのばらつきを表す指標であり、データが平均値からどれくらい離れているかを示します。STDEV関数は、数値の集合を受け取り、それらの数値の標準偏差を返します。
STDEV関数の使い方
STDEV関数は、次のような形式で使用します:STDEV(数値1, 数値2, …)。引数として、標準偏差を計算するための数値を指定します。数値はカンマで区切って複数指定できます。
- 数値1, 数値2, …:標準偏差を計算するための数値。
- カンマで区切って複数の数値を指定できます。
- 少なくとも2つの数値を指定する必要があります。
STDEV関数の注意点
STDEV関数を使用する際には、次のような注意点があります。
- 引数として指定した数値が2つ未満の場合、エラーが返されます。
- 引数にテキストや論理値が含まれている場合、それらは無視されます。
- 空のセルは無視されますが、0の値は計算に含まれます。
STDEV関数の応用例
STDEV関数は、次のような場面で応用できます。
- 統計解析において、データのばらつきを評価するために使用します。
- 品質管理の分野で、製品の品質のばらつきを把握するために使用されます。
- 金融分野で、投資のリスクを評価する際に、収益率の標準偏差を計算するために使用します。
Excelで標本サイズを求める関数は?

Excelで標本サイズを求める関数は、SAMPLE関数です。この関数を使用すると、与えられた母集団から特定の個数の標本をランダムに抽出することができます。
SAMPLE関数の使い方
SAMPLE関数は、次のような書式で使用します。
=SAMPLE(母集団範囲, 標本サイズ)
- 母集団範囲: 標本を抽出するデータ範囲を指定します。
- 標本サイズ: 抽出する標本の個数を指定します。
SAMPLE関数の注意点
- SAMPLE関数は、Excel 365以降で使用可能です。
- 抽出された標本は重複を許容しないです。つまり、同じデータが複数回抽出されることはありません。
- 標本サイズが母集団のサイズよりも大きい場合、エラーが返されます。
標本サイズの決定方法
標本サイズの決定には、標本誤差や信頼水準などが考慮されます。
- 標本誤差: 母集団パラメータの推定値と真の値との差です。標本サイズが大きいほど、標本誤差は小さくなります。
- 信頼水準: 標本統計量が母集団パラメータをどの程度正確に推定しているかを示す指標です。一般的には95%や99%の信頼水準が用いられます。
- 標本サイズの求め方には、ズーメスの公式やフィッシャーの正確検定など、さまざまな方法があります。
よくある質問
標準偏差を求めるためのExcelの関数は何ですか?
Excelで標準偏差を求めるためには、STDEV.S関数またはSTDEV.P関数を使用します。STDEV.S関数は、標本標準偏差を計算するために使われます。一方、STDEV.P関数は、母集団標準偏差を計算するために使用されます。これらの関数を正確に使い分けることで、データのばらつきを正確に把握することができます。
Excelで標準偏差を求める計算式は何ですか?
Excelで標準偏差を求める計算式は、データの平均値から各データを引いた値の2乗の平均の平方根です。具体的には、=SQRT(SUM((データ範囲-平均値)^2)/(データ数-1))という式を使用します。この式を用いることで、データの散らばり具合を数値で表すことができます。
STDEV.S関数とSTDEV.P関数の違いは何ですか?
STDEV.S関数とSTDEV.P関数の主な違いは、標本標準偏差と母集団標準偏差の計算方法にあります。STDEV.S関数は、データが標本であると仮定し、分母にデータ数-1を使用します。一方、STDEV.P関数は、データが母集団全体であると仮定し、分母にデータ数を使用します。この違いにより、同じデータに対しても、計算結果が若干異なることがあります。
Excelで標準偏差を求める際の注意点は何ですか?
Excelで標準偏差を求める際の注意点は、データの選択と関数の選択です。データの選択では、分析対象となるデータ全体を正確に選択することが重要です。また、関数の選択では、データが標本なのか母集団なのかを判断し、適切な関数(STDEV.SまたはSTDEV.P)を使用することが大切です。これらの点に注意することで、正確な標準偏差の計算が可能になります。

私は、生産性向上に情熱を持つデータ分析とオフィスツール教育の専門家です。20年以上にわたり、データ分析者としてテクノロジー企業で働き、企業や個人向けのExcel講師としても活動してきました。
2024年、これまでの知識と経験を共有するために、日本語でExcelガイドを提供するウェブサイト**「dataka.one」**を立ち上げました。複雑な概念を分かりやすく解説し、プロフェッショナルや学生が効率的にExcelスキルを習得できるようサポートすることが私の使命です。